Binary Representation of Integers: Direct, Inverse & Two’s Complement

In this lesson, we will briefly examine how integer numbers are stored in computer memory and what direct, inverse, and two’s complement codes are.

Numbers in computer memory are stored in binary form. Suppose we have a byte type. A byte consists of eight bits. The binary representation of a byte value in memory looks like this:

The most significant bit (leftmost bit) in signed integers is used to indicate the sign. For positive numbers, it is always 0. For negative numbers, the most significant bit is always 1. This representation of numbers in binary is called the direct code.

The following table shows numbers in the decimal system and their corresponding binary format:

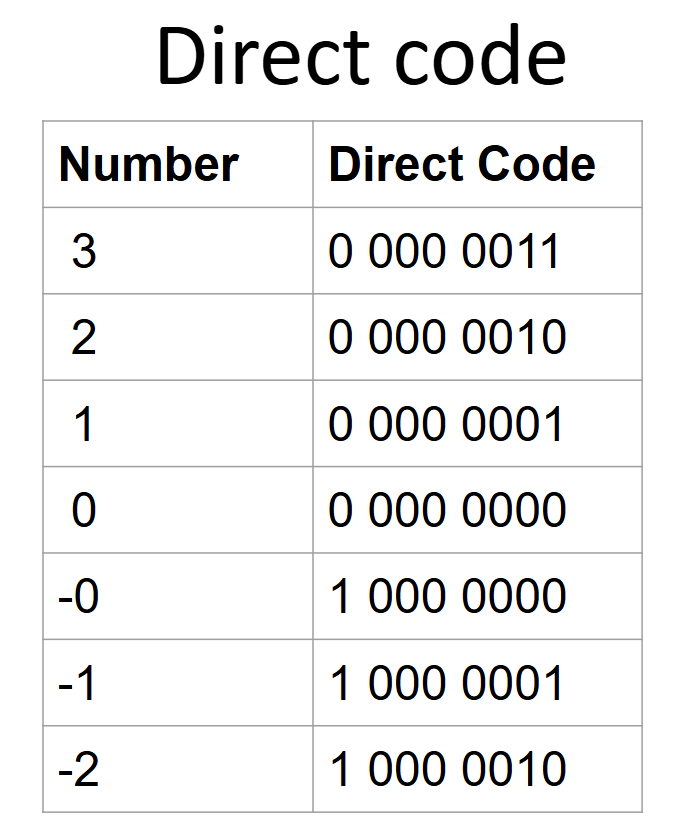
Thus, in the binary system, using direct code, a seven-bit number can be stored in an eight-bit memory cell (byte).

However, in computing, direct code is primarily used for representing positive numbers.

For negative numbers, the so-called two’s complement code is used. This is due to the convenience of performing arithmetic operations with numbers in electronic computing devices.

The following algorithm is used to convert a negative number to two’s complement code:

1. All bits of the number (except for the first bit) are inverted, i.e., replaced with their opposites (0 becomes 1, and 1 becomes 0):

   

2. Next, add one to the inverted number:
   

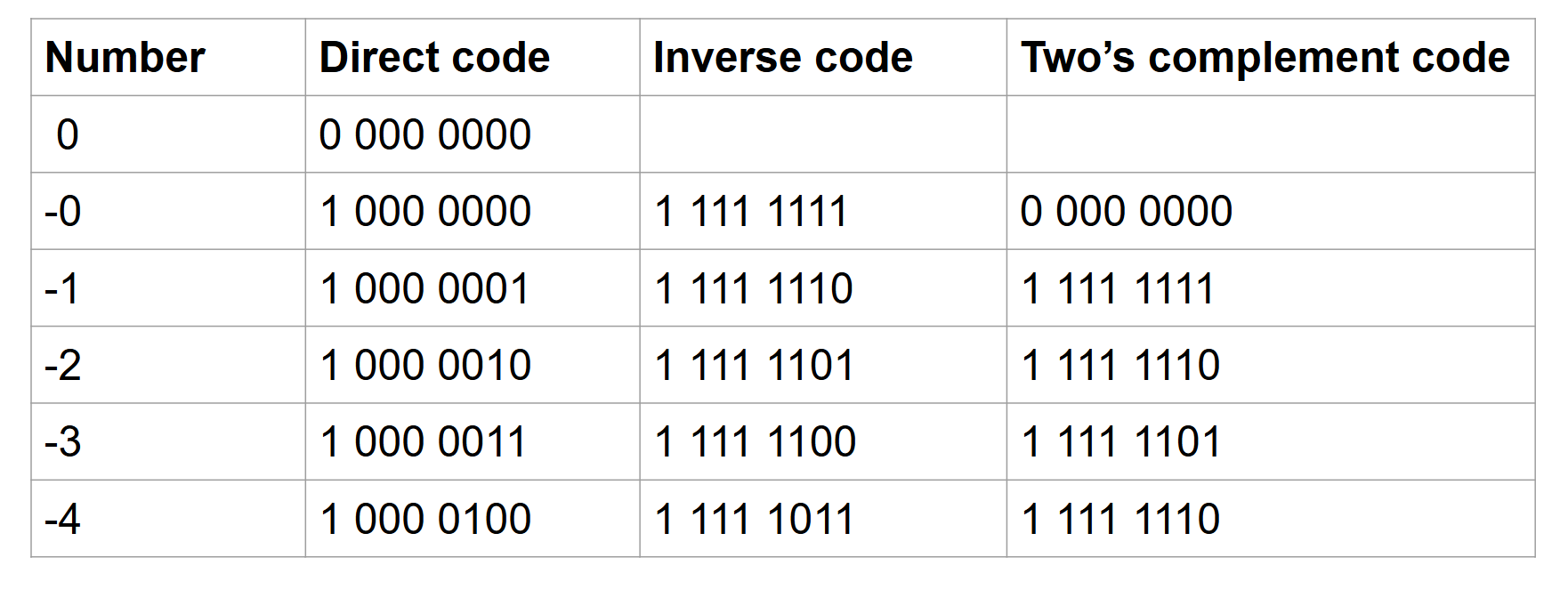
The following table presents the direct, inverse, and two’s complement codes for negative numbers. In inverse code, there is a small issue: we end up with two zeros. There is both 0 and -0, and they have different values. However, in two’s complement code, zero has the same value as in direct code:

Курс 'Java для начинающих' на Udemy