Вычисление сложности алгоритма

Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти.

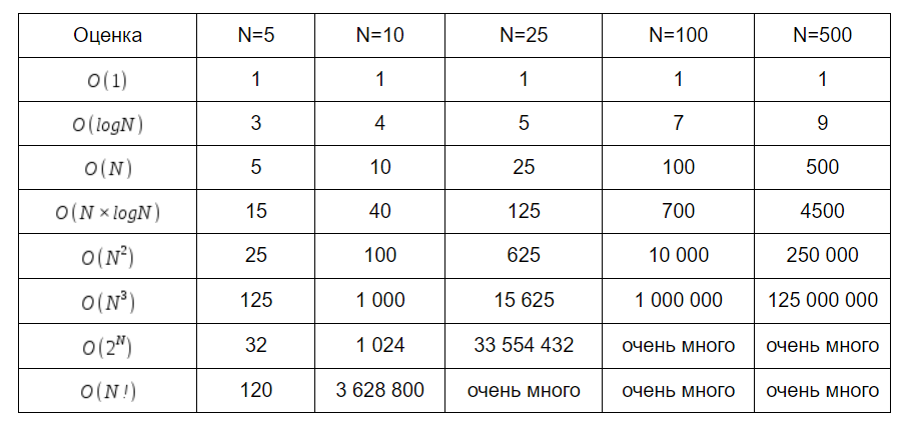
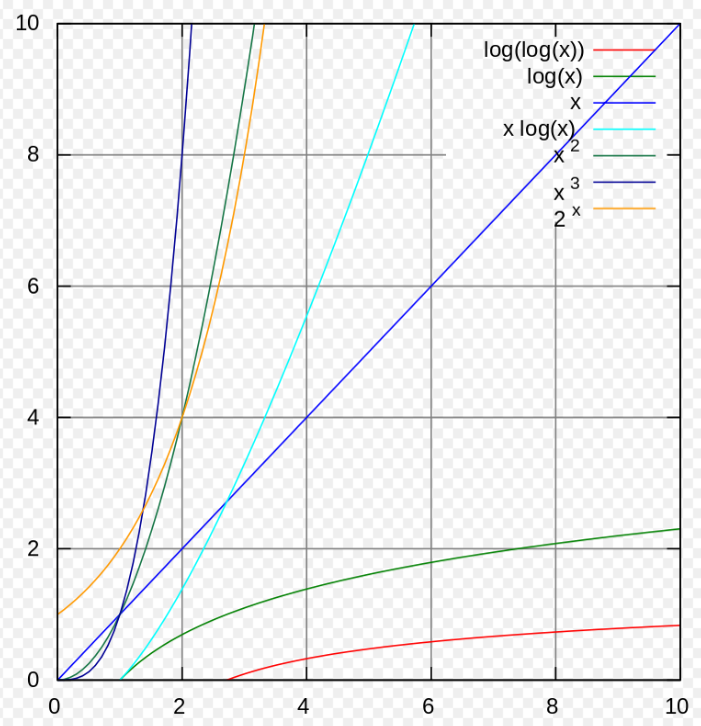
Асимптотическая сложность - это сложность при стремлении размера входных данных к бесконечности. Сложность описывается обычно с помощью буквы O. Примеры:

O(1) – константная сложность
O(n) - линейная сложность
O(log n) - логарифмическая сложность
O(n*log(n)) - квазилинейная сложность
O(n2) - квадратичная сложность
O(2^n) - экспоненциальная сложность.

Сложность алгоритма

График роста

Правила использования большого O:

Константы игнорируются. Например:

8n^4 =O(n^4)

(n^2)/5=O(n^2)
В выражениях учитывается только самая быстрорастущая функция, потому что при очень большом n, только она будет иметь значение:

n^2+n=O(n^2)

2^n+n^9=O(2^n)
Основание логарифма не пишется, так как они отличаются на константу: O(log()n).