Primitive Types and Literals in Java
1. Introduction
In this article, we will examine primitive types and literals in Java. Types in Java are divided into two categories: primitive (simple, basic) and reference (object) types. Reference types include arrays, classes, and interfaces.
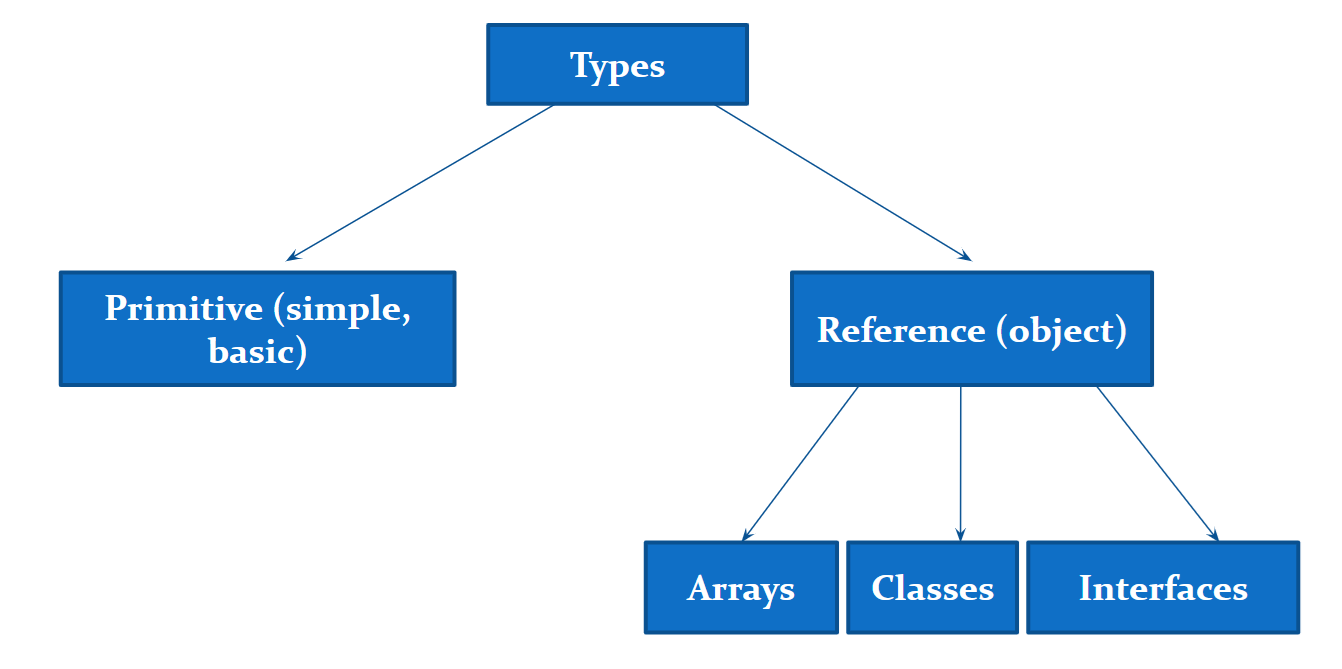
In this section, we will focus only on primitive types.
Primitive types in Java are predefined and named using keywords.
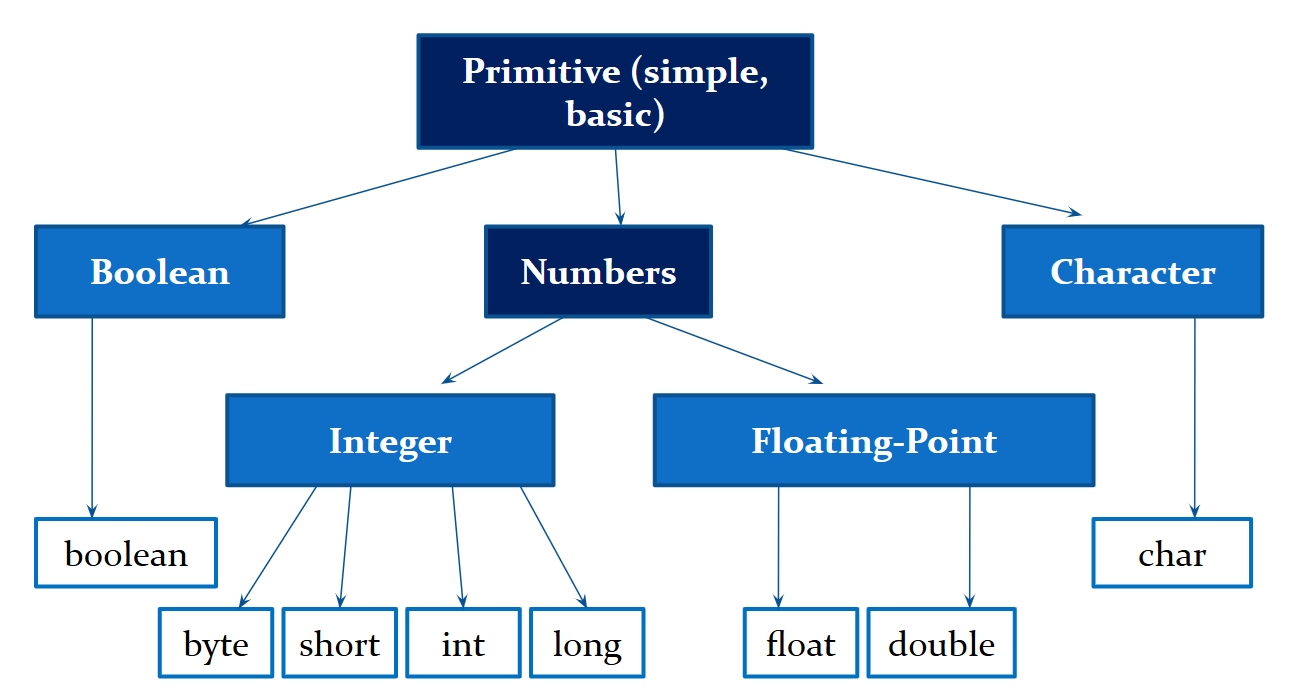
Primitive types can be divided into the following four groups:
-
Integers. This group includes the data types
byte,short,int, andlong, representing signed integers. -
Floating-Point Numbers. This group includes the data types
flоаtanddouble, representing numbers with precision up to a specified number of decimal places. -
Characters. This group includes the
chardata type, which represents characters, such as letters and digits, from a specific set. -
Boolean Values. This group includes the
booleandata type, specifically designed for representing logical values.
The following table contains information about the length, range of allowable values, and default values of primitive types:
| Type | Size in Bytes | Size in Bits | Possible Values (from … to) | Default Value |
|---|---|---|---|---|
| boolean | — | 1 | true or false | false |
| byte | 1 | 8 | -128..127 | 0 |
| short | 2 | 16 | -32,768..32,767 | 0 |
| int | 4 | 32 | -2,147,483,648..2,147,483,647 | 0 |
| long | 8 | 64 | -9,223,372,036,854,775,808..9,223,372,036,854,775,807 | 0 |
| char | 2 | 16 | 0..65,535 | '\u0000' |
| float | 4 | 32 | -3.4E+38..3.4E+38 (IEEE 754 standard) | 0.0 |
| double | 8 | 64 | -1.7E+308..1.7E+308 (IEEE 754 standard) | 0.0 |
2. Integer Types
Let’s start with integer types. Integer numbers in Java are represented by four types: byte, short, int, and long. The first question that everyone inevitably asks is—why so many? The integer types differ in size in bytes and, of course, in possible values. Depending on the data you need to store, you choose one of these types.
byte – used for transmitting data over the network, reading from and writing to files. It is typically not used in mathematical operations.
short – the least commonly used type in Java, it may be used only for memory optimization purposes.
int – the primary integer type, used by default in Java. So if you are unsure which type to choose, go with int. Any integer number will be treated by the compiler as an int type. It is commonly used for loop counters, array indices, and character indices in strings.
long – an integer type containing a virtually infinite range of values. It is used when numbers exceed 2 billion and the standard int type is no longer sufficient. It is commonly used in everyday applications for creating unique values.
As you can see, the default value for all these types is zero. All numeric types are signed, meaning they can have both negative and positive values:
| Type | Size in Bytes | Size in Bits | Possible Values (from..to) | Default Value |
|---|---|---|---|---|
| byte | 1 | 8 | -128..127 | 0 |
| short | 2 | 16 | -32,768..32,767 | 0 |
| int | 4 | 32 | -2,147,483,648..2,147,483,647 | 0 |
| long | 8 | 64 | -9,223,372,036,854,775,808..9,223,372,036,854,775,807 | 0 |
Now let’s look at an example of declaring and initializing integer primitive types:
byte b = 4;
short s1 = 7, s2 = 5;
int i1 = 56, i2;
i2 = 78;
long a1 = 456;The value that comes after the equals sign is called a literal. In some sources, it is also referred to as a constant, but I will stick to the term literal.
Integer literals can be of several types:
- decimal
- octal
- hexadecimal
- binary – starting from Java 7
What does that mean? See, there are different numeral systems.
2.1 Decimal Literals
That is, the numeral system we are used to is decimal. It uses 10 digits to represent a number – from 0 to 9.
Let’s consider decimal integer literals, which are familiar values to us. A minus sign is used to indicate negative numbers. Also, you can place a plus sign as shown below for the variable x3, but this is optional:
int x1 = 878;
int x2 = +878;
int x3 = -878;2.2. Octal Literals
In the octal numeral system, there are eight digits: from 0 to 7. To indicate that the number is in octal, a zero is placed at the beginning of such a value. For example:
int six = 06; // Equals the decimal number 6
int seven = 07; // Equals the decimal number 7
int eight = 010; // Equals the decimal number 8
int nine = 011; // Equals the decimal number 9
System.out.println("eight: " + eight);
System.out.println("nine: " + nine);When we print these values to the console, they are always displayed in decimal format:
eight: 8
nine: 92.3. Hexadecimal Literals
- Hexadecimal literals are created using the following characters
[0-9a-fA-F] - They must start with
0xor0X. - Up to 16 characters can be used in hexadecimal numbers, excluding the
0xprefix and the optionalLsuffix.
For example:
int a1 = 0X0005;
int a2 = 0x7ddfffff;
int a3 = 0xcccccccc;2.4. Binary Literals in Java 7
To define a binary literal, add the prefix 0b or 0B to the number. Only 0 and 1 are used. For example:
int i1 = 0b101;
int i2 = 0B101; All integer literals represent int values. If the literal value falls within the byte, short, or char range, it can be assigned to a variable of that type without casting.
To create a long literal, you must explicitly specify it by appending an 'l' or 'L' at the end. However, it’s better to use uppercase L since lowercase l looks very similar to the number one:
long a1 = 220433L;
long a2 = 0x3FFl;When might this be necessary? Suppose you have a large number that does not fit into the int range.
2.5. Underscores in Numeric Literals
Starting from Java 7, the ability to use any number of underscores to separate groups of digits has been added to improve readability.
Underscores can only separate digits! They cannot be used in the following places:
- At the beginning or end of a number
- Next to the decimal point in floating-point numbers
- Before
'F','f','l', or'L'suffixes - To separate prefix characters
int i1 = 12_567; // OK
double d1 = 56.356_234; // OK
short s = 0b000____0100; // OK
int i2 = 220_; // Compilation error
int i3 = 0_x2F; // Compilation error
int i4 = 0x_3E; // Compilation error
float f1 = 6345.56_f; // Compilation error
float f2 = 3423_.87f; // Compilation error3. float and double Types
Floating-point numbers (or real numbers) are represented by the float and double types. They are used to store values with precision up to a certain number of digits after the decimal point:
| Type | Size in bytes | Size in bits | Possible values (from..to) | Default value |
|---|---|---|---|---|
| float | 4 | 32 | -3.4E+38..3.4E+38 (IEEE 754 standard) | 0.0 |
| double | 8 | 64 | -1.7E+308..1.7E+308 (IEEE 754 standard) | 0.0 |
double — these are double-precision numbers, as close as possible to the specified or computed values. Used in Java for any mathematical computations (square root, sine, cosine).
float — a less precise floating-point type. Used less frequently for memory-saving purposes.
Let’s look at an example of declaring primitive floating-point types. All floating-point literals are assigned the double type by default. To separate the fractional part, a dot is used, not a comma. If your integer is zero, you can omit the zero and just write .4:
double d1 = 145454545.676767676;
double d2 = .4;// number 0.4If you want to create a float literal, you must specify an F (uppercase or lowercase) at the end of the literal. In the following example, three variables f1, f2, and f3 are created:
float f1 = 56.45455; // Compilation error
float f2 = 343434.454563F;
float f3 = 78.45f;For variable f1, no F is specified at the end, meaning the literal is of type double. Therefore, a compilation error will occur. f2 and f3 are correctly specified with F at the end.
Also, to explicitly indicate that our literal is of type double, we can add a D (uppercase or lowercase) at the end, but this is not required. For example, as done with variables d3 and d5:
double d3 = 454545.454545D;
double d4 = 654.321;
double d5 = 54.32d;double d6 = 1.5e14; // The value of this number is 1.5*10^14
double d7 = 1.5E+14; // The value of this number is 1.5*10^14
double d8 = 1.5e-14; // The value of this number is 1.5*10^-14In Java, there are three special floating-point numbers used to represent overflow and errors:
- Positive infinity - the result of dividing a positive number by 0. Represented by constants
Double.POSITIVE_INFINITYandFloat - Negative infinity - the result of dividing a negative number by 0. Represented by the constants
Double.NEGATIVE_INFINITYandFloat.NEGATIVE_INFINITY. NaN(Not a Number) - the result of 0/0 or taking the square root of a negative number. Represented by the constantsDouble.NaNandFloat.NaN.
Example of using special floating-point numbers in arithmetic expressions:
public class Main {
public static void main(String[] args) {
int a = 7;
double b = 0.0;
double c = -0.0;
double g = Double.NEGATIVE_INFINITY;
System.out.println(a / b);
System.out.println(a / c);
System.out.println(b == c);
System.out.println(g * 0);
}
}Floating-point numbers should not be used in financial calculations where rounding errors are unacceptable. For example, the result of the expression System.out.println(2.0 - 1.1) will be 0.8999999999999999, not 0.9 as one might logically expect. Such errors are due to the internal binary representation of numbers. Just as it is impossible to represent the result of 1/3 exactly in decimal, it is also impossible to represent the result of 1/10 exactly in binary. If rounding errors need to be eliminated, the BigDecimal class should be used.
4. boolean type
| Type | Size in bytes | Size in bits | Possible values (from … to) | Default value |
|---|---|---|---|---|
| boolean | — | 1 | true or false | false |
The primitive type boolean is used to store logical values. Logical variables of this type can only take two values: true – true and false – false. Memory required for a variable of this type is 1 bit.
Example of declaring boolean variables:
boolean b1 = false;
boolean b2 = true;The following example of initializing a boolean variable is incorrect. In some programming languages, 0 and 1 are used for boolean literals. In Java, this is not possible – it will not compile:
boolean b3 = 0; 5. char type
| Type | Size in bytes | Size in bits | Possible values (from … to) | Default value |
|---|---|---|---|---|
| char | 2 | 16 | 0..65,535 | '\u0000' |
Characters are described by the char type in Java. This type has a size of 2 bytes.
Let's look at character literals that we can use to initialize these variables. The first option for defining character literals is to use single characters. In the following example, we assign the character in single quotes. For example, variable c1 will contain the character 'n', and variable c2 will contain the character '#':
char c1 = 'n';
char c2 = '#';
We can also assign character literals using Unicode values since the char type in Java supports Unicode. In this case, we use not the character itself but the numeric value of the character. This is why the char type is also called a pseudo-integer type. But these values can only be positive. As we will see in future lessons, we can even apply arithmetic operations to the char type.
For each character in the Unicode table, which contains all letters, numbers, and special characters, there is a corresponding code. With this type, we can represent a single character. In Java, we can specify this code using any number system. But if we look at the Unicode table, we will see that the values are given in hexadecimal format:
char letterO = '\u004F'; // Letter 'O' in hexadecimal form
char letterA = '\141'; // Letter 'a' in octal form
char a1 = 0x675; // Hexadecimal integer literal
char a2 = 345; // Decimal integer literal However, when printing any of these variables to the console, the values will be displayed as characters.
For example, when executing this code:
char c2 = 97;
System.out.println(c2);it will print
aSome character literals use the backslash for escape sequences. For example, if we want to set a quote symbol, we must escape it using the backslash:
char c1 = '\''; If we want to set a newline character, we do it like this:
char c2 = '\n';The third option where we can use the backslash is for tabulation:
char c3 = '\t';6. String literals
In this lesson, we will also look at string literals, although, of course, strings are not primitive types.
- String literals are denoted by enclosing the sequence of characters in double quotes, unlike character literals, which use single quotes.
- Control characters and octal or hexadecimal notation defined for character literals also work the same way in string literals.
String str1 = "MyProgram";
String str2 = "first line\nsecond line";
String str3 = "\"This is in quotes\"";
String str4 = "\u004F letter";//O letter
Please log in or register to have a possibility to add comment.